Lab 11: Graphs

In this lab, you will develop a routing algorithm to securely send data between state capitals. Each state capital building has a government-approved router, but not all capitals are directly connected. Only state capitals of bordering states are connected. Given a source state and a destination state, you will use Dijkstra’s algorithm to calculate the shortest path (in kilometers) for transmitting the data, with the route passing only through the capitals of bordering states. For example, a secure message from Albany, NY to Annapolis, Maryland could follow one of these paths:

• (Albany, NY -> Trenton, NJ -> Dover, DE -> Annapolis, MD)
• (Albany, NY -> Harrisburg, PA -> Annapolis, MD)

However the path (Albany, NY -> Dover, DE -> Annapolis, MD) would not be valid, as New York and Delaware do not share a border.

You will implement a Graph where each state is represented as a vertex. The edges between vertices represent connections between bordering states, with edge weights indicating the distance between capitals.

Objectives:

1. Implement Graphs using Adjacency Lists
2. Implement Dijkstra’s Algorithm
3. Working with built-in Java data structures

By the end of this lab, I hope you will have gained a deeper understanding of graphs and reachability algorithms through hands-on experience.

Allowed Imports: You may import any data structure from java.util, except for the Graph class or any of its subclasses. This includes collections such as List, LinkedList, ArrayList, Map, HashMap, TreeMap, PriorityQueue, and others. If you are unsure whether you can use a specific data structure, please ask the instructor.

Files You’ll Be Working With

All files to download are available at: https://bmc-cs-151.github.io/labs/lab11/. Just append the file name to that URL and use wget to download.

Download:

1. Download the graph interface Graph.java which specifies the methods you will implement along with Vertex.java and Edge.java.
2. Download Util.java. This contains a helper method to print your graph, and a helper method getDistance to calculate the distance in kilometers between two city capitals. It also contains scaffolding and a helper class for Dijkstra’s algorithm.
3. Download the data files us-state-capitals.csv and bordering-states.csv

Exercise 1: Implement Graphs as Adjacency Lists

Start by creating a AdjacencyListGraph.java that implements the Graph interface you downloaded. In an adjacency list each vertex of the graph is associated with a list of outgoing edges.

For the following graph (adapted from lecture)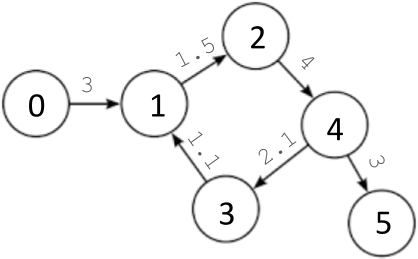: the adjacency lists would be as follows:

• 0: [Edge(3, 1)]
• 1: [Edge(1.5, 2)]
• 2: [Edge(4, 4)]
• 3: [Edge(1.1, 1)]
• 4: [Edge(2.1, 3), Edge(3, 5)]
• 5: []

Think about which data structure(s) you should use to keep track of this mapping from vertices to outgoing edges. In your README, describe which data structure(s) you chose and why.

Implement the required methods as specified in the Graph interface.

Be sure to include a default constructor for autograding.

Exercise 2: Represent State Data as a Graph

In this section of the lab, you will be working with the csv data files you downloaded.

The first file: us-state-capitals.csv contains a row for each state capital and its longitude and latitude data. In the second file, bordering-states.csv, the 1st column indicates the state and the following columns indicate the states it borders.

You will implement a Graph where each state is represented as a vertex. The edges between vertices represent connections between bordering states, with edge weights indicating the distance between capitals.

I recommend you do this in the following steps:

1. Create a file named DriverLab11.java where you will implement the solution. Start by creating an empty AdjacencyListGraph. Then, read in the us-state-capitals.csv file, which contains information about the U.S. states and their capital location. You will need a State class to store the state’s name, latitude, and longitude. Be sure to include a getName() method for autograding. Once you’ve created the State objects, add them to the graph as vertices.

2. Next, read the border information, which will serve as the edges between states. Each row in the border file will provide two states and the distance between them. Use the Haversine formula to calculate the distance between these states (you can find the formula and its implementation in Util.java). Add an edge between the corresponding vertices (states) in the graph, using the calculated distance as the edge weight. When inserting edges, ensure that there are no duplicates. (You may need to implement .equals() methods for both the State and Edge classes if needed).

3. Once you’ve added all the vertices and edges, use the printGraph method from the Util class to print the graph and verify its correctness. The graph should show each state with outgoing edges to the states it borders. If you find any duplicate edges, consider revisiting your equals() methods to handle the comparison properly. Finally, once you’re confident the graph is accurate, comment out the call to printGraph to avoid unnecessary output.

Exercise 3: Implement the Shortest Path Algorithm (Dijkstra’s)

In this part, will prompt the user for the source and destination state and output the shortest path between the two. Here are some sample inputs and outputs:

Ready to transmit!

Where are we starting from? 
New York
Where are we sending the data? 
Maryland

Sending a total distance of: 503.98km

Where are we starting from?
Illinois
Where are we sending the data?
Mississippi

Sending a total distance of: 1016.67km

Exit the program by using return (DO NOT USE SYSTEM.EXIT) if the user types exit.

Start by implementing Dijkstra’s algorithm in Util.java. The algorithm works by maintaining a collection of the shortest known distances to each vertex, which it gradually refines. Starting from the source, it explores the closest vertices first, updating their distances as shorter paths are found. The process continues until all reachable vertices have been processed, ensuring the shortest path to each one is discovered. Use the pseudocode from lecture as a starting point. Before you begin coding, think about what data structures you will need:

1. A collection to store the shortest known distances from the source to each vertex. Initially, the source vertex will have a distance of zero and all other vertices will have infinity (use Double.MAX_VALUE in your implementation as a proxy for infinity). This structure should have efficient lookups to quickly retrieve the current shortest known distance to a vertex. It should also have efficient updates to update the known distance if a shorter path to a vertex is found.

2. A collection to keep track of vertices that have already been processed, so they are not revisited. Once a vertex has been “settled” (i.e., the shortest path to it has been found), it is added to this data structure. It should have efficient insertions and lookups.

3. A priority queue (min-heap) to efficiently select the next vertex to explore - the one smallest tentative distance. This structure should have efficient poll operations to quickly retrieve and remove the vertex with the smallest distance. For this collection, use Java’s builtin java.util.PriorityQueue.

By carefully choosing and managing these structures, you’ll be able to efficiently compute the shortest path from the source to the destination. Discuss your choices for (1) and (2) in the README. Both should be builtin Java data structures. Consult this table for a list of builtin Java data structures.

Defining the Ordering of Priority Queue Elements:

In Dijkstra’s algorithm, elements in a priority queue need to be ordered by their distance from the source node. The priority queue ensures that the node with the smallest distance is processed first. In the case of a min heap, each node must be smaller than its children.

To define what “smaller” means for vertices in our graph, we look at the Node class in Util. Each Node wraps a Vertex and includes a double dist field, which represents the distance from the source (the starting state capital in our example). When implementing Dijkstra’s algorithm, the priority queue will store these Node objects, and it will remove them based on their dist values—ensuring that the vertex with the shortest distance from the source is processed first.

Now that you have your data structures defined, start from the pseudocode in lecture and fill in dijkstra. Do not ask ChatGPT to fill in this method in entirety - the autograder will run plagiarism detection if the method and its structure were purely written by AI.

Once you are confident that your algorithm is correct, finish up your driver by prompting the user for source and destination state, and printing the total distance returned by dijkstra.

The csv files will be passed as command line arguments in the following order: DriverLab11 us-state-capitals.csv bordering-states.csv

Submitting your Assignment for Grading

Submit your code to gradescope where it will be autograded.

What to submit:

1. README with the following:

   (a) Your name and how long the assignment took you.

   (b) What data structure did you use for your adjacency list and why?

   (c) What data structures did you use to track visited vertices and the current distances from the source, and why?

2. AdjacencyListGraph.java
3. Util.java
4. DriverLab11.java
5. State.java
6. Any other files you created (no need to upload Graph, Edge, or Vertex.java)

Grading: This assignment will be extra credit (up to 10% points on your final exam).